Smoothing EEMs
Data pretreatment is a critical part of any PARAFAC analysis of fluorescence EEMs. All EEMs contain so-called Rayleigh and Raman scatter that does not represent organic matter fluorescece and does not behave trilinearly.
Why? While each fluorophore has only one emission and one exctation spectrum (at constant conditions), scatter does not. With each excitation wavelength, scatter light changes its emission properties. Thus, you would need at least one component for each type of scatter and each excitation wavelengh measured in your dataset to model Raman and Rayleigh scatter. This is why we like to remove scatter before modeling organic matter fluorescence.
Unfortunately, the extend to which such disturbing scatter is present varies between datasets. This tutorial will show you:
- How to determine how much scatter each particular dataset contains
- Which functions of the drEEM toolbox can be used for this problem
- How to refine the parameters for smoothing
The sections of this tutorial
- What is Rayleigh and Raman scatter?
- Loading the data & creating the dataset
- Inspect your EEM, locate the scatter
- Determine scatter excision parameters
- Refining the scatter excision
- To interpolate or not to interpolate?
- Evaluating our result
- The summary
You can select the bits of code, paste them into a MATLAB, and run them yourself. All necessary materials are provided with the drEEM toolbox. Note: In this tutorial, I will show condensed code where the output of one function is immediately fed to another function without creating an intermediate variable.
Example. These two sections produce the same result:
x2=function1(x1);
x_final=function2(x2);
% The same in one line:
x_final=function2(function1(x));
What is Rayleigh and Raman scatter?
Rayleigh scatter
Rayleigh scatter is a type of elastic scatter. Photons from the excitation source bounce off molecules in solution, after which they are scattered in many directions without a loss of energy. Some of this scatter makes its way into the detector. Most importantly, Rayleigh scatter always appears at exactly the same wavelength as the light currently selected for excitation. So in your EEM, Rayleigh scatter will appear on a 1:1 Ex:Em line (e.g. 250:250nm).
Raman scatter
Raman scatter is a type of inelastic scatter. Compared to Rayleigh scatter, a much smaller portion of photons from the excitation source impact molecules and are inelastically scattered (most abundantly the solvent, in our case water). During inelastic scattering, some of the energy of the photos is transfered, and the resulting scatter appears at a wavelength different to that of the excitation wavelegnth.
For futher in depth reading, I can highly recommend this paper.
Most importantly for this tutorial: Where will the scatter be located in your EEMs?
Now that we know what to expect, we can start by loading EEMs and creating a dataset.
Loading the data & creating the dataset
First let’s intialize our MATLAB session:
clearvars
cd '...\\drEEM'
dreeminstall
Then, load the data and cut some of the noisy and unreliable wavelengths:
load PortSurveyData_corrected.mat
mydata= assembledataset(XcQS,Ex,Em_in,'QSE','site',sites,...
'rep',replicates,'longID',filelist_eem,...
'ID',sampleID,'cruise',cruises,'date',dates,[]);
Xstart=subdataset(mydata,[],mydata.Em>580,mydata.Ex<250);
clearvars -except Xstart
Inspect your EEM, locate the scatter
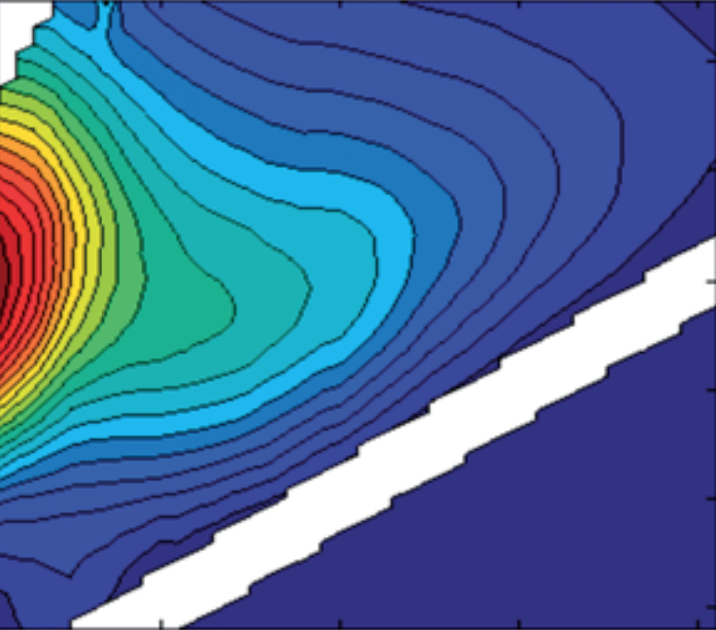
Take a look at the EEMs.
eemreview(Xstart,'samples',10)
The diagonal lines of high signals in the EEM represent scatter that does not represent organic matter fluorescence. They are problematic, since these diagonal features cannot be modeled using PARAFAC. They do not behave trilinearly.
So, we have to cut these scatter signals out and
- leave the diagonal missing, or
- interpolate over it.
We use the function smootheem to handle scatter.
But which types of scatter are present & how much do we cut out?
The function eemreview allows us to calculate that exactly.
After calling eemreview(Xstart), click ‘Spectra’ and point the cross at ex = 280nm.
The emission spectrum will then show us 1st order Raman and 1nd order Rayleigh scatter in detail.
Determine scatter excision parameters
While it is tempting to try and cut all scatter at once, I recommend an approach in which you attempt to address at most two of the maximum number of four scatter types at once. That allows you to focus on a smaller number of problems at a time and address them appropriately. It’s worth spending a little more time in the beginning, because you save it by not having to go back to this step.
Which scatter diagonals to address first and in which sequence does not matter. Here, I address the most severe scatter first.
Part 1: 1st order Raman, 2nd order Rayleigh
Use the data cursor tool in MATLAB to locate the Raman (black line) and Rayleigh (red line) scatter in the bottom right emission spectrum. They should be at 309.3 and 560nm.
Now find the wavelength where the Rayleigh and Raman scatter peaks become undistinguishable from the DOM signals.
- For the Raman peak (1st order, black) those points are 298 and 318nm. These are:
- 309-298 = 11nm below the predicted scatter location
- 318-309 = 9nm above predicted Raman scatter peak
- For the Rayleigh peak (2nd order, red) those points are 546 and 574nm. These are:
- 560-546 = 14nm below
- 574-560= 16nm above predicted Rayleigh scatter peak.
Let’s see how the EEMs look once these two diagonal scatter bands are removed.
We use smootheem to remove scatter.
Note where exactly I paste the data from the analysis above in the smootheem function.
Type help smootheem for further reading.
For each type of scatter, you must specify how much to cut below, then above of the predicted position of the scatter [above below]:
eemreview(smootheem(Xstart,[ ],[9 11],[16 14],[ ],[0 0 0 0],[],3382,0))
The results look not bad at all, even though 2 of the 4 scatter types have not yet been removed. Leaving some of the inputs emtpy simply leaves the scatter unhandled.
Part 2: 1st order Rayleigh
Do you notice how the excitation spectrum in the image above shows zeros around the Rayleigh scatter line (red, towards the right in the top right graph)?
Those zeros have probably been introduced artefitially during or before the data import. Some manufacturer sofware’s offer to handle scatter by replacing it with zero’s.
However, zero’s can be just as problematic as scatter itself. The organic matter fluorescence underneath the scatter was also zero’ed. Zero’s don’t adequatly represent organic matter fluorescece. Thus, these zero’s need to be removed.
At Ex = 446, the scatter line appears at 446nm in the emission spectrum. Data above 440nm goes to zero abruptly.
- 446 - 440 nm = 6 nm (below the predicted scatter).
What about above? Hard to tell, right?
For that, we must look somewhere else. The emission spectrum at Ex = 295nm shows that information!
The Rayleigh scatter appears at 295nm. Data until 302nm is zero.
- 302 - 295nm = 7 nm (above the predicted scatter).
Together with the previous settings, I add the new information:
eemreview(smootheem(Xstart,[7 6],[9 11],[16 14],[ ],[0 0 0 0],[],3382,0))
Now there are no traces of arteficial zero’s or scatter in the 1st order Rayleigh region:
Part 3: 2nd order Raman
The region around the 2nd order Raman scan looks ‘strange’. The contour lines are not smooth, but it is rather hard to make out a diagonal line of scatter.
Since there is not much data around the scatter line, it’s also hard to judge the extent of the problem.
Are there any samples that show the scatter to a larger extent?
Yes. it turns out that sample 7 features a lot of 2nd order Raman scatter:
From the plots, it appears that the Raman scatter is not quite where we would predict it. It is located at slightly longer wavelengts!
The emission spectrum at ex = 255nm predicts the Raman (2nd order) at 558.1nm.
The scatter disappears at 554nm below and extends at least until Em = 578nm.
- 558 - 554 = 4nm (below setting), and
- 578 - 558 = 20nm (above setting).
Let’s try these settings:
eemreview(smootheem(Xstart,[7 6],[9 11],[16 14],[20 4],[0 0 0 0],[],3382,0))
Refining the scatter excision
Looking though some of the EEMs, these settings seem to remove the scatter well, but some scatter is left over in others.
You can use the function scanview to judge whether all scatter is gone. It plots EEMs as a series of emission spectra.
DOM fluorescence is smooth and broad. Any scatter leftovers will show up as drastic increases in fluorescence.
But if you have many samples, inspecting each EEM is tedious. How could we make this easier?
The function spectralvariance may help us. It visualizes the variance across all samples.
Most importantly for this tutorial, it summarizes the variance in one single plot (a standard deviation EEM). That’s
much easier compared to flicking through hundreds of EEMs.
Since scatter varies a lot, it will be very obvious in the resulting plot:
spectralvariance(smootheem(Xstart,[7 6],[9 11],[16 14],[20 4],[0 0 0 0],[],3382,0))
The function warns us that some EEMs have very little overall fluorescence. Let’s remove them and look at the output again:
Xtemp=subdataset(smootheem(Xstart,[7 6],[9 11],[16 14],[20 4],[0 0 0 0],[],3382,0),[7:10 86:89],[],[])
spectralvariance(Xtemp)
clearvars Xtemp
The product looks better now.
There are issues with the 1st order Rayleigh scatter. There is clearly some leftover on both edges:
It appears to be equal on both sides, so lets add 5 below and 5 above:
Xtemp=subdataset(smootheem(Xstart,[7+5 6+5],[9 11],[16 14],[20 4],[0 0 0 0],[],3382,0),[7:10 86:89],[],[])
spectralvariance(Xtemp)
clearvars Xtemp
That worked well. Now that this issue has dissapeared, we can see a small issue with the 1st order Raman scatter.
There is still some leftover scatter signal in some samples (below the cut diagonal).
Let’s add 5nm, but only below:
Xtemp=subdataset(smootheem(Xstart,[7+5 6+5],[9 11+5],[16 14],[20 4],[0 0 0 0],[],3382,0),[7:10 86:89],[],[])
spectralvariance(Xtemp)
clearvars Xtemp
After that issue is solved, the spectral variance plot reveals leftover scatter in the range of 2nd order Raman scatter.
Just like before, there is some leftover scatter below what was alread cut out.
Again, we can try to add 10nm (it’s a bit more this time around).
Xtemp=subdataset(smootheem(Xstart,[7+5 6+5],[9 11+5],[16 14],[20 4+10],[0 0 0 0],[],3382,0),[7:10 86:89],[],[])
spectralvariance(Xtemp)
clearvars Xtemp
The end product of spectralvariance looks quite good:
To interpolate or not to interpolate?
Are we ready to PARAFAC now? Not so fast, let’s look at the EEM. Specificially, there’s a list of things we should consider:
- Are there scans in the EEM that only contain missing numbers (that we cut out) or zeros (inserted below the 1st order Rayleigh by
smootheem)? - Is there a large triangle of missing numbers in the upper left corner of the EEM?
- How much data is there between 1st and 2nd order Raman and Rayleigh, respectively?
Consider the following for these questions:
- We can see in the above image that the low emission scans barely contain any viable, actual fluorescence data. We should cut some of the emission and start at ~300nm where there is acutal data. Otherwise, PARAFAC does not have a “truth” to compare against.
- There is a small triangle of missing numbers in the upper left corner, but there should be enough data for PARAFAC to fit components. Watch out for this range when fitting models.
If components look strange in this wavelength range, consider that you may have to cut the entire emission range that encompasses the triangle using
subdataset - Looks like there is enough data between both 1st and 2nd order scatter types. Again, inspect the components carefully and react once you spot an issue.
Last question: Should we interpolate over the scatter types?
To answer, consider what is needed for interpolations. We need good data below and above each scatter type.
If there are no good signals, the interpolation will not work nicely.
Replacing missing numbers is desirable for PARAFACing in general (discussed here, but consider that replacing the scatter bands with an interpolation guess puts real numbers into an EEM that were not measured.
If your interpolation does not work well, there is a chance that PARAFAC picks up on the strangeness of the interpolation, giving some components unnatural loadings. But remember that there are no ultimate answers; each case might be different.
It generally PARAFAC does pretty well in guessing what numbers should have been there due to the trilinear structure of the model / data, so you are always free to try modeling your dataset without interpolating over scatter. Just be aware where the missing numbers were originally located, and remember to look out for the spectral loadings of your components in these areas.
Let’s consider our dataset. It makes no sense interpolating the 2nd order Raman scatter since there are no numbers left above the scatter. But we can try all other scatter types:
Xtemp=subdataset(smootheem(Xstart,[7+5 6+5],[9 11+5],[16 14],[20 4+10],[1 1 1 0],[],3382,0),[7:10 86:89],[],[])
spectralvariance(Xtemp)
clearvars Xtemp
The result:
Juding whether or not this worked well is quite subjective and one of the many reasons why PARAFAC analysis has not yet been automated.
You can clearly see that the interpolation produces some artefacts that stemm most likely from noisy samples.
In the original PARAFAFC tutorial, all scatter was interpolated.
For the purpose of this tutorial, I chose not to interpolate. Te final result looks pretty good:
Evaluating our result
We have our final settings. Now, we can try out PARAFAC to see if any obvious issues appear:
ds=subdataset(smootheem(Xstart,[12 11],[9 16],[16 14],[20 14],[0 0 0 0],[],3382,0),[7:10 86:89],[Xstart.Em<300],[])
models=prandinitanal(ds,2:5,2,'nonnegativity',1E-6);
This certainly takes a while, even with parallel computing. Therefore, I only ran 2 initializations per number of components.
You should always run more initializations to make sure you have really found the global minimum.
Here, my aim of PARAFAC’ing this dataset is not to obtain the ultimate solution, but just to see if a quick analysis revleals some obvious issue connected to leftover scatter.
The resulting model does not indicate any scatter issues and the components look somewhat similar to those in the 2013 tutorial paper. However, a complete PARAFAC analysis requires more steps that are described in the tutorial in more detail.
The summary
These MATLAB code lines summarize the final result of this tutorial:
clearvars
cd '...\\drEEM'
dreeminstall
load PortSurveyData_corrected.mat
mydata= assembledataset(XcQS,Ex,Em_in,'QSE','site',sites,...
'rep',replicates,'longID',filelist_eem,...
'ID',sampleID,'cruise',cruises,'date',dates,[]);
Xstart=subdataset(mydata,[],mydata.Em>580,mydata.Ex<250);
clearvars -except Xstart
Xend=smootheem(Xstart,[12 11],[9 16],[16 14],[20 14],[0 0 0 0],[],3382,0);
% Optional
Xend=subdataset(Xend,[7:10 86:89],Xend.Em<300,[])
Remember that the challenges change from dataset to dataset. So your own dataset will require a unique approach that will differ from this tutorial.