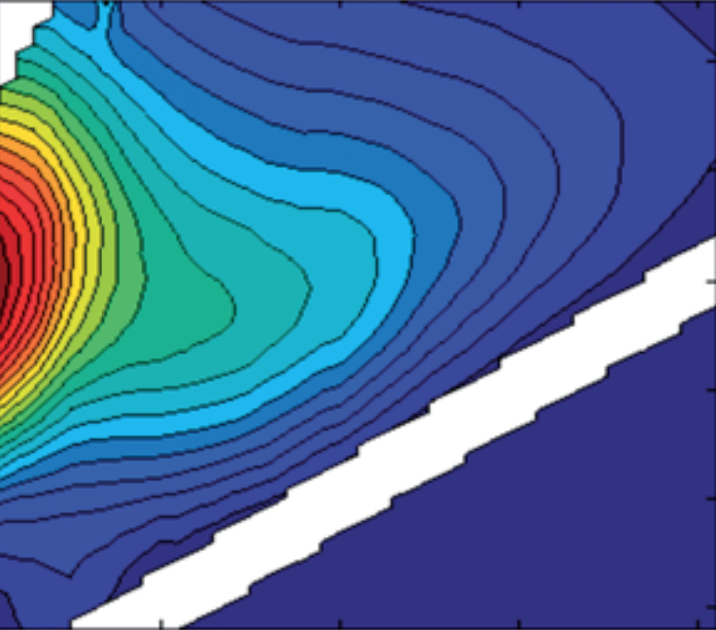
PARAFAC on EEMs
PARAFAC tutorial (pure fluorophores)
The previous tutorial has been removed and will be replaced in the coming weeks. Thank you for your patience. Please be aware that the toolbox documentation in MATLAB contains tutorials that are accessible via drEEMtoolbox.doc(“drEEM”)